왜 loss function으로 mean squared error를 사용할까

Linear regression을 처음 배울 때, loss function으로 mean squared error를 사용한다고 배운다.

그리고 이것에 대해 많은 자료들은 loss function에 제곱을 사용하는 이유는 단지 실제 데이터와 예측 데이터 간의 차이를 나타내기 위함이라고 설명하고 넘어간다.

그러나 차이를 나타낼 수 있는 수많은 함수들 중 왜 하필 제곱을 사용하는 지에 대해 언급하는 자료는 많지 않다.

왜 절댓값, 네제곱 등이 아닌 제곱을 사용할까?

결론부터 얘기하면, 실제 값과 예측된 값의 차이(error)가 gaussian distribution을 따른다고 가정하고, 이러한 error가 나올 likelihood를 maximize하는 모델을 만드는 것이 linear regression이기 때문이다.

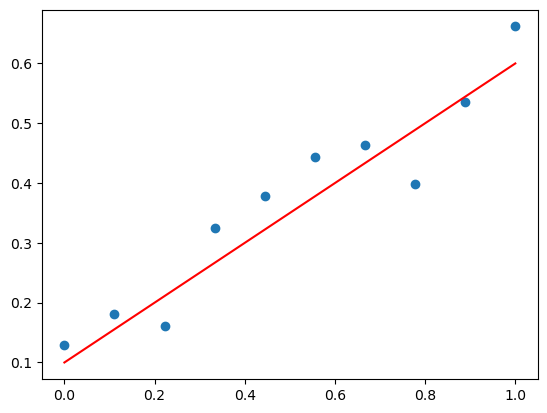
위와 같은 데이터에 대해 linear regression을 수행한다고 하자.

Linear regression을 하게 되면, 실제 데이터 값 $y$와 우리가 예측하는 데이터값 $\hat{y}$ 간의 차이, $\text{error} = y - \hat{y}$ 이 존재할 것이다.

우리는 이 error가 gaussian distribution을 따른다고 가정한다.

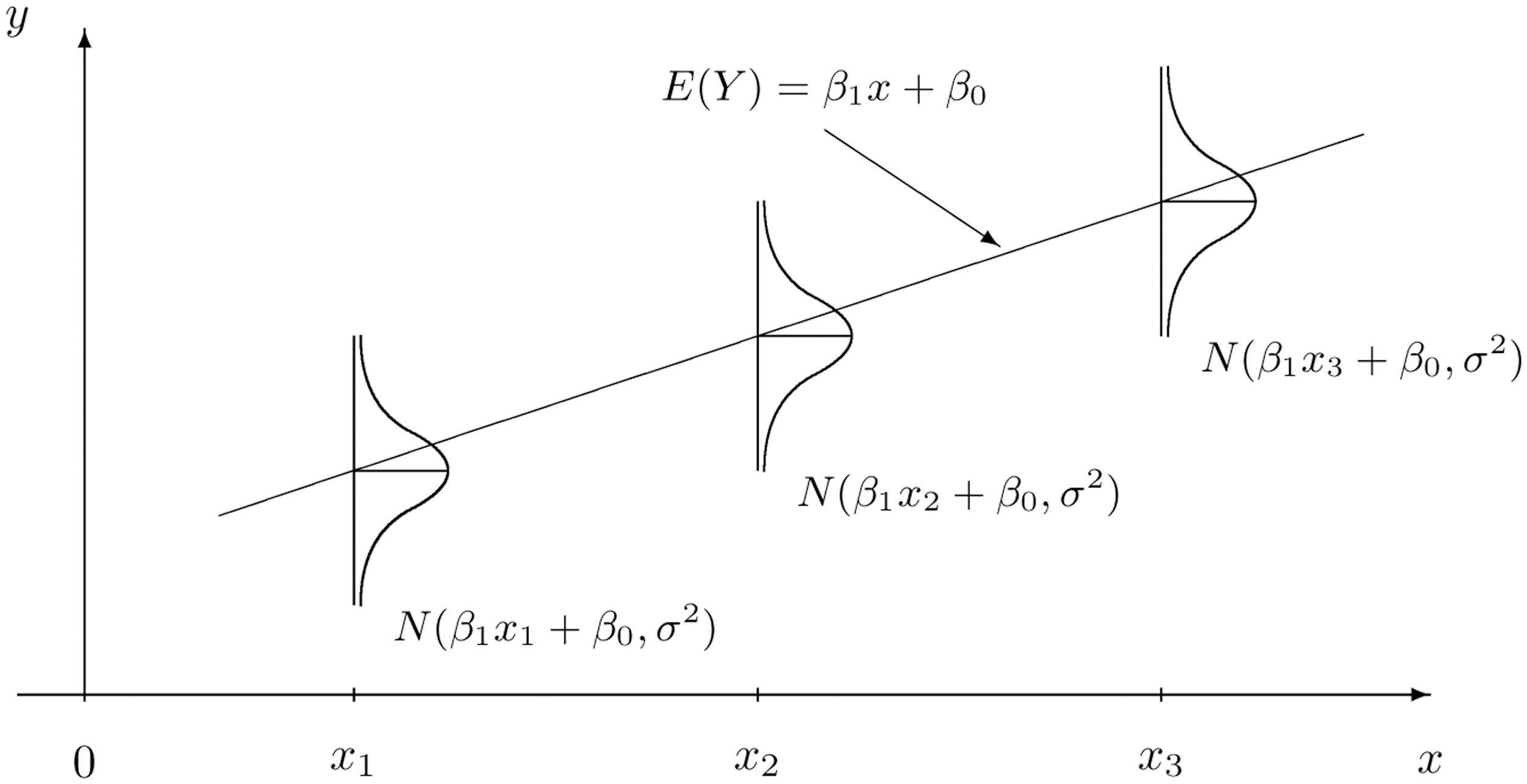
위 그림과 같이 우리가 예측하는 함수 $\hat{y} = \beta_1 x + \beta_0$ 라 하자.

그렇다면 데이터 $x_1$ 에 대해 우리가 예측하는 결과값은 $\hat{y_1} = \beta_1 x_1 + \beta_0$ 이다.

실제값 $y_1$ 과 예측값 $\hat{y_1}$ 간의 차이가 gaussian distribution을 따른다고 가정했으므로, error $\epsilon \sim \mathcal{N}(0, \sigma^2)$​ 이라고 하자.

여기서 $\epsilon = y_1 - (\beta_1 x_1 + \beta_0)$ 이므로 $y_1\sim \mathcal{N}(\beta_1 x_1 + \beta_0, \sigma^2)$​ 이라고 할 수 있다.

그렇다면 우리의 예측을 바탕으로 실제 결과값 $y_1$​​ 이 나올 확률은 아래와 같다.

\[f(y_1 | \beta_1 x_1 + \beta_0, \sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{(y_1 - (\beta_1 x_1 + \beta_0))^2}{2\sigma^2}}\]

$y_2,: y_3,…,: y_n$ 에 대해서도 같은 방법으로 확률을 구할 수 있다.

따라서 error 값이 gaussian distribution을 따른다고 가정하면, $y_1,: y_2,…, : y_n$​​ 이라는 데이터가 나올 likelihood는 아래와 같다.

\[\text{likelihood} = \prod\limits_{i=1}^{n} \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{(y_i - (\beta_1 x_i + \beta_0))^2}{2\sigma^2}}\]

우리는 궁극적으로 이 likelihood를 maxmimize하는 $\hat{y} = \beta_1 x + \beta_0$​ 을 찾고 싶은 것이다.

Log는 단조증가 함수이기 때문에, likelihood를 maximize 하는 것은 negative log likelihood를 minimize하는 것과 같다.

여기서 굳이 log를 붙이는 이유에는 크게 두 가지가 있다.

1. Likelihood 값이 너무 작아져 컴퓨터가 잘못 처리하는 것을 방지하기 위해.
2. 곱셈을 덧셈으로 바꾸기 위해.

또한 negative를 붙이는 것은 (0~1) 사이인 likelihood 값에 log를 씌워 음수가 된 것을 다시 양수로 바꾼 후, 이를 loss로 취급하여 최소화하기 위함이다.

위에서 likelihood 식을 negative log likelihood로 바꾸면 아래와 같다.

\[\text{NLL} = \sum \limits_{i=1}^{n} \frac{1}{\sqrt{2\pi \sigma^2}} \frac{(y_i - (\beta_1 x_i + \beta_0))^2}{2\sigma^2}\]

이를 최소화하는 $\beta_0, \beta_1$​ 를 찾는 것이 목표이며, 아래와 같이 표현할 수 있다.

\[\hat{\beta_0}, \hat{\beta_1} = \underset{\beta_0, \beta_1}{\operatorname{argmin}} \: \text{NLL} = \underset{\beta_0, \beta_1}{\operatorname{argmin}}\sum \limits_{i=1}^{n} \frac{1}{\sqrt{2\pi \sigma^2}} \frac{(y_i - (\beta_1 x_i + \beta_0))^2}{2\sigma^2} = \underset{\beta_0, \beta_1}{\operatorname{argmin}}\sum \limits_{i=1}^{n} {(y_i - (\beta_1 x_i + \beta_0))^2}\]

$\sigma$ 가 있는 부분을 없앨 수 있는 이유는 NLL을 최소화하는 $\beta_0, \beta_1$ 값은 $\sigma$ 값에 상관없이 같기 때문이다.

정리하면, linear regression은 negative log likelihood $\sum \limits_{i=1}^{n} {(y_i - (\beta_1 x_i + \beta_0))^2}$ 을 최소화하는 $\beta_0, \beta_1$​ 을 찾는 것이다.

그렇기 때문에 이를 평균한 값, 즉 mean square error를 loss 함수로 사용하는 것이다.